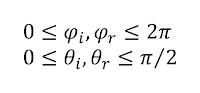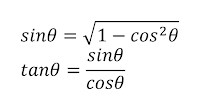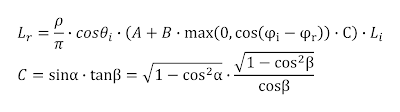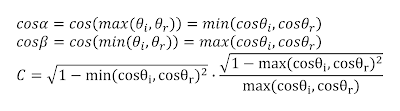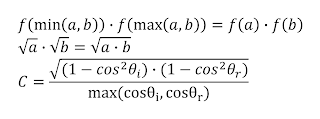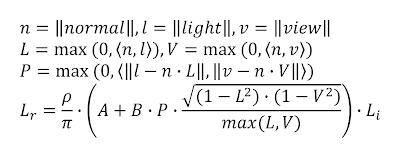van Ouwerkerk's rewrite (of the Oren Nayar BRDF)

Introduction
M. Oren and S.K. Nayar proposed a diffuse BRDF in Generalization of Lambert's Reflectance Model, Michael Oren, Shree K. Nayar, July 1994, Siggraph, pp. 239-246 that takes the roughness of a surface into account. This BRDF is often cited as too slow for realtime use, because of the sin and tan instructions in the equation. In this post I present a rewritten version of the equation which I'd like to call "van Ouwerkerk's rewrite". The rewritten equation evaluates significantly faster on modern GPU's, making it more feasible to use the Oren Nayar BRDF in realtime applications.

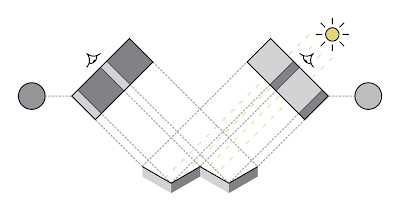Figure 1 - backscattering towards light source in V-cavities

The Oren Nayar BRDF is based on mathematical analysis of light interacting with a surface consisting of V-cavities. In their work they predict that roughness results in more light being reflected back in the direction of the light source, which is illustrated in figure 1. This backscatter effect is contained in the resulting simplified Oren Nayar BRDF listed in equation 1.

Equation 1 - (simplified) Oren Nayar BRDF

Angle range

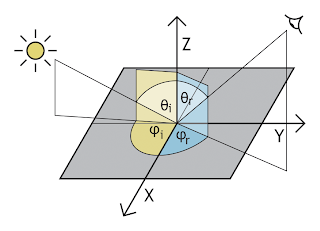Figure 2 - graphical overview of angles

The incoming light direction is described by the angles θi and φi, while the reflected light direction is described by the angles θr and φr as illustrated in figure 2. The azimuth angles are described by φi and φr in a full circle from 0 to 2π on the plane of the surface. The zenith angles described by θi and θr are therefore always positive and range from 0 to π. Since light can't illuminate a surface from the back and we can't see a surface from the back, θi and θr are constrained to a meaningful range of 0 to π/2 as made explicit in equation 2.

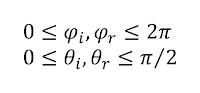Equation 2 - angles constrained to meaningful range

Trigonometric identities
Our goal is to remove the sin and tan instructions from the Oren Nayar BRDF. Since a cos can often be replaced by a much faster dot product, we start by transforming the sin and tan instructions into cos instructions using the two trigonometric identities listed in equation 3. Note that the square root would mathematically have both a positive and a negative result. Since the zenith angles are constrained to the 0 to π/2 range, we can assume the positive result.

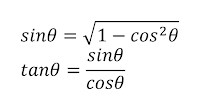Equation 3 - trigonometric identities

This will transform the BRDF into the expanded form listed in equation 4. For easier reading, the part with the original sin and tan instructions is split into a separate part C of the equation.

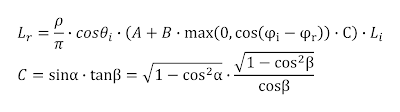Equation 4 - application of trigonometric identities

Alpha and beta

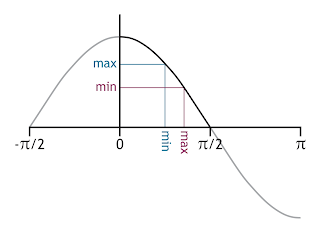Figure 3 - cosine from 0 to π/2

The dot product of two normalized vectors equals the cosine of the angle between them. This identity is very often used in computer graphics. The problem that arises with the Oren Nayar BRDF is that the angles α and β can't be readily expressed as an angle between two vectors. This prevents the use of a dot product instead of the more expensive cos instruction. In order to overcome this, we'll have to remove the min and max instructions inside the cos. If we look at the cosine function we see that it is strictly decreasing in the 0 to π/2 range as illustrated in figure 3. We can use this to move the min and max instructions outwards as listed in equation 5.

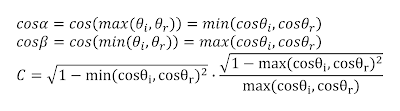Equation 5 - moving min and max outwards

Minimum and maximum
Since both the minimum and the maximum of the incoming and reflected zenith angles are processed in the same way, we can apply another simplification as listed in equation 6. If one of the angles is the minimum, the other one is automatically the maximum. This means we can replace the mirrored min and max instructions with the two parameters contained in them. We can also combine the two square roots into one.

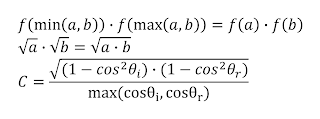Equation 6 - mirrored min and max

Vector math
At this point we can replace all cosine functions with dot products and transform the equation into the vector math commonly found in realtime shaders. The final result is listed in equation 7.

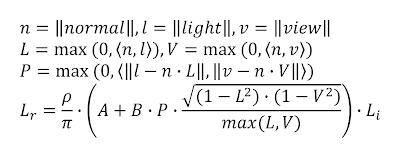Equation 7 - van Ouwerkerk's rewrite

Implementation
The proposed equation is implemented in an HLSL pixel shader as shown in the listing below. The determination of the surface albedo and the amount of incoming light is not included in this listing as it depends on many other factors.

// Input vectors
float3 normal = normalize(input.normal);
float3 light = normalize(input.light);
float3 view = normalize(input.view);
// Roughness, A and B
float roughness = input.roughness;
float roughness2 = roughness * roughness;
float2 oren_nayar_fraction = roughness2 / (roughness2 + float2(0.33, 0.09));
float2 oren_nayar = float2(1, 0) + float2(-0.5, 0.45) * oren_nayar_fraction;
// Theta and phi
float2 cos_theta = saturate(float2(dot(normal, light), dot(normal, view)));
float2 cos_theta2 = cos_theta * cos_theta;
float sin_theta = sqrt((1-cos_theta2.x) * (1-cos_theta2.y));
float3 light_plane = normalize(light - cos_theta.x * normal);
float3 view_plane = normalize(view - cos_theta.y * normal);
float cos_phi = saturate(dot(light_plane, view_plane));
// Composition
float diffuse_oren_nayar = cos_phi * sin_theta / max(cos_theta.x, cos_theta.y);
float diffuse = cos_theta.x * (oren_nayar.x + oren_nayar.y * diffuse_oren_nayar);

Final words
I've hereby presented a faster way to evaluate the Oren Nayar BRDF specifically targeted at usage in realtime shaders. This document has been submitted as proposal to the GPU Pro 3 book.

Introduction to HLSL - Part 3

• Part 2

Diffuse lighting
In this part we're going to add some simple diffuse lighting. The new lines compared to the previous part are marked in bold.

// 1: Application inputs

float4x4 object_to_world: WORLD;

float4x4 object_to_clip: WORLDVIEWPROJECTION;

float3 light_pos: LIGHT_POS;
float3 light_color: LIGHT_COLOR;

float3x3 object_to_world3x3 = (float3x3)object_to_world;

// 2: Structures

struct vs_in {

   float4 pos_object: POSITION;

   float3 normal_object: NORMAL;

};

struct ps_in {

   float4 pos_clip: POSITION;

   float3 normal_world: TEXCOORD0;

   float3 light_world: TEXCOORD1;

};

// 3: Vertex Shaders

ps_in vs_main(vs_in input) {

   ps_in output;

   output.pos_clip = mul(input.pos_object, object_to_clip);

   output.normal_world =
      mul(input.normal_object, object_to_world3x3);

   float4 pos_world = mul(input.pos_object, object_to_world);

   output.light_world = light_pos - pos_world.xyz;

   return output;

}

// 4: Pixel Shaders

float4 ps_main(ps_in input) : COLOR {
   float3 result = light_world;

   float3 normal_world = normalize(input.normal_world);

   float3 light_world = normalize(input.light_world);

   result *= saturate(dot(normal_world, light_world));

   return float4(result, 1.f);

}

// 5: Techniques

technique main {

   pass p0 {

      VertexShader = compile vs_3_0 vs_main();

      PixelShader = compile ps_3_0 ps_main();

   }

}

In this example we add the normals (in object space) as inputs to the vertex shader. The vertex shader turns them into world space. Note that the full 4-by-4 transformation matrix includes translation, rotation and scale. For the transformation of normals we are only really interested in the rotation, so we use a reduced 3-by-3 matrix for the transformation. The vertex shader also calculates the vector from the surface of the object to the light source (in world space) and passes this information on to the pixel shader.

Introduction to HLSL - Part 2

• Part 1

Our first shader
In this part we take the two critical lines of the last part (marked bold) and turn it into a complete HLSL shader. In this introduction I target Shader Model 3.0 which is compatible with DirectX 9.0c.

// These are comments
// 1: Application inputs

float4x4 object_to_clip: WORLDVIEWPROJECTION;

// 2: Structures

struct vs_in {

   float4 pos_object: POSITION;

};

struct ps_in {

   float4 pos_clip: POSITION;

};

// 3: Vertex Shaders

ps_in vs_main(vs_in input) {

   ps_in output;

   output.pos_clip = mul(input.pos_object, object_to_clip);

   return output;

}

// 4: Pixel Shaders

float4 ps_main(ps_in input) : COLOR {

   return float4(1.f, 1.f, 1.f, 1.f);

}

// 5: Techniques

technique main {

   pass p0 {
      VertexShader = compile vs_3_0 vs_main();
      PixelShader  = compile ps_3_0 ps_main();
   }

}

The shader code consists of 5 parts. The application inputs, the structures used (for input and output), the vertex shader(s), the pixel shader(s) and the technique(s). The vertex shader is executed for each vertex in the model and does the minimum it has to do, transform the model into clip space. The pixel shader is executed for each pixel and simply returns a fully opaque white pixel in this case. In the next part we'll add some diffuse lighting.

• Part3

Introduction to HLSL - Part 1

Naming conventions
 

In programming it's good practice to name your variables logically. Often I see this practice not executed in shader writing. That's why I'm starting with some variable naming conventions I like to adhere to. One of the most basic things a shader has to do is to transform the rendered object from object space into clip space. I'll come back to mathematics behind this, but for now it's enough to know that this transformation can be done by a single matrix multiplication. The matrix in question has the input semantic WORLDVIEWPROJECTION. The code for the transformation is commonly written as:

float4x4 wvp: WORLDVIEWPROJECTION;
out.pos = mul(in.pos, wvp);

In this code we find two distinct variables that are both named pos. The one in the in structure is the position in object space, while the one in the out structure is the position in clip space. The first naming convention I adhere to is to add the space a vector is in as a suffix. So we update the transformation above into this one:

float4x4 wvp: WORLDVIEWPROJECTION;

out.pos_clip = mul(in.pos_object, wvp);

Next lets look at the variable wvp. These three letters are a logical shorthand of WorldViewProjection, but what is the function of this variable in our code? We will almost always use this matrix to convert a vector from object space into clip space. So we'll call the variable object_to_clip instead. We'll also lengthen in and out a little bit to input and output:

float4x4 object_to_clip: WORLDVIEWPROJECTION;

output.pos_clip = mul(input.pos_object, object_to_clip);

This concludes the first part of the introduction to HLSL. In the next part we'll take this must have piece of code and extend it into our first full HLSL shader.

• Part 2